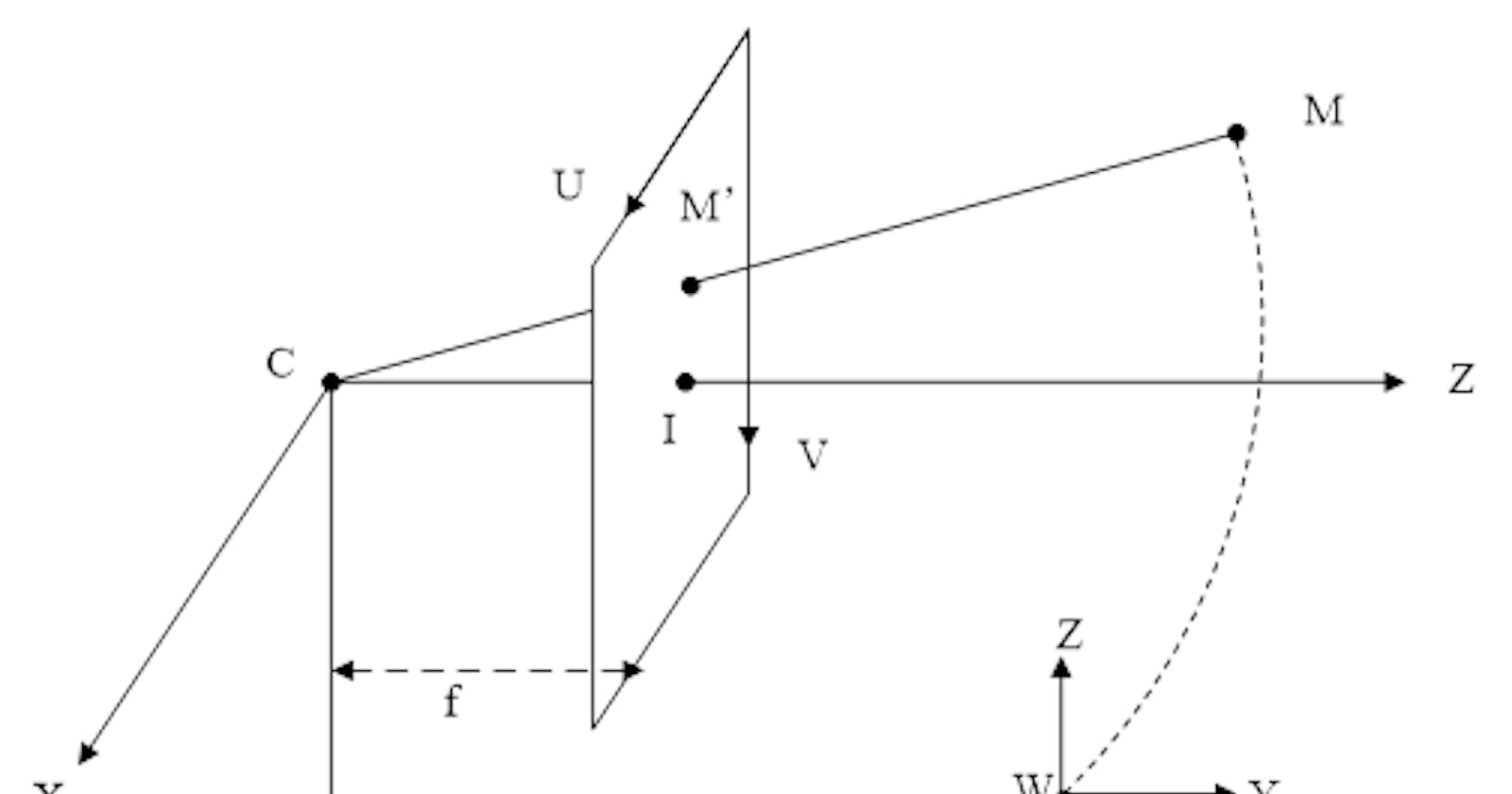
相机标定
相机标定的意义
相机标定是将物体二维图片中的位置关系反映射回三维空间中的方法。
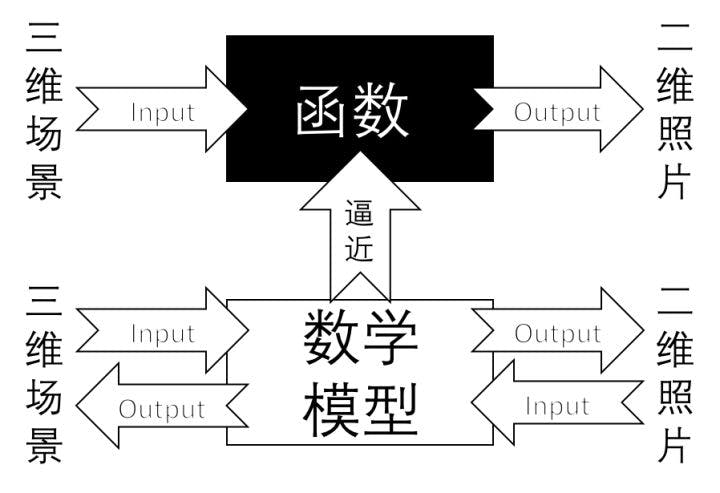
图片来自于许翔翔的知乎专栏
为了能够获得这种映射关系,我们需要求出摄像机参数的几何模型,总的来说可以划分为相机的内参和外参以及畸变参数。
通过相机标定,我们能够:
- 对相机的畸变进行校正
- 通过像素值获取真实值
- 实现坐标系统
几个重要的坐标系
在进行相机标定前,我们需要先了解一下几个重要的坐标系,分别为:
- 像素坐标系
- 图像坐标系
- 相机坐标系
- 世界坐标系
像素坐标系 P(u,v)
像素坐标系是指物体在相片中的像素的位置。
该坐标系的原点位于图片的左上角,宽高范围分别为图像的宽高像素。
如图中的P0。
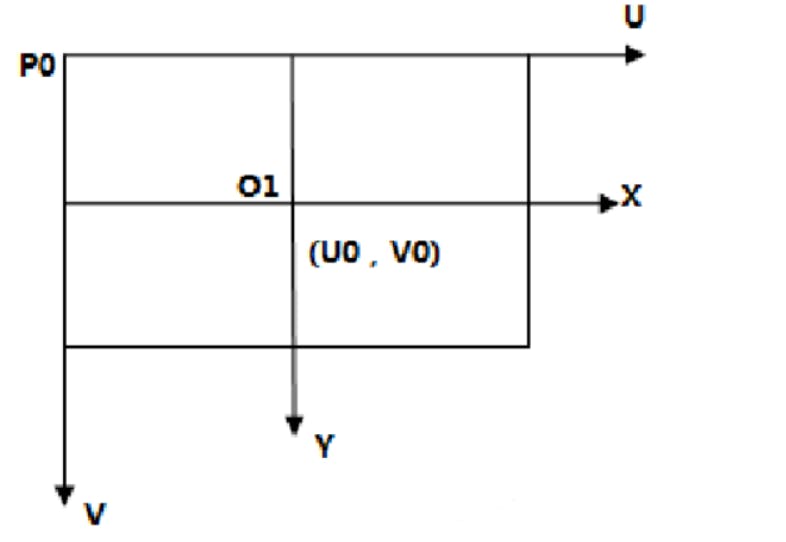
图像坐标系 I(x,y)
图像坐标系是指物体在图像中呈现出的相对位置。因图像是2D平面,因此无Z轴。
该坐标系的原点位于图像的中心O1 $(u_0,v_0)$ 处。
相机坐标系 C(x,y,z)
原点为光心的, XY轴方向与图像坐标系同向的坐标系,Z轴方向与图像坐标系垂直。
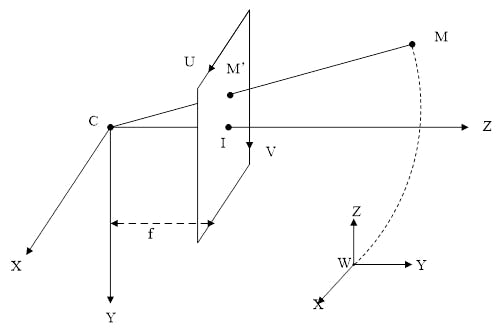
世界坐标系 W(x,y,z)
现实世界的三维空间。
因相机在放置时可能有一定的倾斜和位移,如图所示。
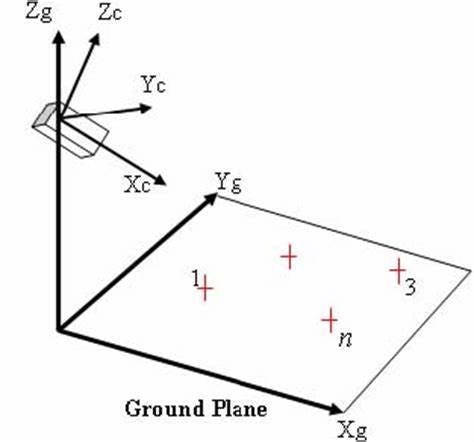
坐标系的转换关系
为获得相片中物体的实际位置,我们需要一步步从像素坐标系转回到世界坐标系。
像素坐标系到图像坐标系
当像素坐标系uv轴垂直时
$$ u = \frac{x}{dx}+u_0 \ v = \frac{y}{dy}+v_0 $$
写成矩阵的形式为
$$ \left[ \begin{matrix} u \ v \ 1 \end{matrix}\right] = \left[ \begin{matrix} \frac1{dx} & 0 & u_0 \ 0 & \frac1{dy} & v_0 \ 0 & 0 & 1 \end{matrix}\right] \left[ \begin{matrix} x \ y \ 1 \end{matrix}\right] $$
当像素坐标系uv存在夹角时
TODO
图像坐标系到相机坐标系
$$ x = f\frac{X_c}{Z_c} \ y = f\frac{Y_c}{Z_c} $$
其中$f$为有效焦距,写成矩阵的形式为
$$ Z_c \left[ \begin{matrix} x \ y \ 1 \end{matrix}\right] = \left[ \begin{matrix} f & 0 & 0 & 0 \ 0 & f & 0 & 0 \ 0 & 0 & 1 & 0 \end{matrix}\right] \left[ \begin{matrix} X_c \ Y_c \ Z_c \1 \end{matrix}\right] $$
此处的$Z_c$即位张正友老师论文中的$s$,是一个任意大小的缩放因子。
像素坐标系到相机坐标系
当uv轴垂直时
$$ Z_c\left[\begin{matrix} u\v\1\end{matrix}\right] = \left[\begin{matrix} \frac1{dx} & 0 & u_0 \ 0 & \frac1{dy} & v_0 \ 0 & 0 & 1 \end{matrix}\right] \left[\begin{matrix} f & 0 & 0 & 0 \ 0 & f & 0 & 0 \ 0 & 0 & 1 & 0 \end{matrix}\right] \left[\begin{matrix} X_c \ Y_c \Z_c \ 1 \end{matrix}\right] $$
记 $$ \bold{K} = \left[\begin{matrix} \frac1{dx} & 0 & u_0 \ 0 & \frac1{dy} & v_0 \ 0 & 0 & 1 \end{matrix}\right] \left[\begin{matrix} f & 0 & 0 \ 0 & f & 0 \ 0 & 0 & 1 \end{matrix}\right] = \left[\begin{matrix} \frac{f}{dx} & 0 & u_0 \ 0 & \frac{f}{dy} & v_0 \ 0 & 0 & 1 \end{matrix}\right] = \left[\begin{matrix} k_x & 0 & u_0 \ 0 & k_y & v_0 \ 0 & 0 & 1 \end{matrix}\right] $$
矩阵$\bold{K}$即为相机内参数矩阵。
当uv轴存在夹角时
TODO
相机坐标系到世界坐标系
世界坐标系和相机坐标系有一定的旋转与平移关系,此处我们引入旋转矩阵$R{3\times3}$和平移向量$T{3\times1}$。
旋转矩阵与平移向量组成的矩阵即为相机的外参数矩阵 $[\begin{matrix}R{3\times3}&T{3\times1}\end{matrix}]$。
相机坐标系转换到世界坐标系的方法写成矩阵形式为
$$ \left[ \begin{matrix} X_c \ Y_c \ Zc \ 1 \end{matrix}\right] = \left[ \begin{matrix} R{3\times3} & T_{3\times1} \ O & 1 \end{matrix}\right] \left[ \begin{matrix} X_w \ Y_w \ Z_w \ 1 \end{matrix}\right] $$
像素坐标系到世界坐标系
综上所述,我们能够将从像素坐标系到世界坐标系的转换表示为:
$$ Zc \left[ \begin{matrix} u \ v \ 1 \end{matrix}\right] = \left[ \begin{matrix} \bold{K}{3\times3} & O \end{matrix}\right] \left[ \begin{matrix} R{3\times3} & T{3\times1} \ O & 1 \end{matrix}\right] \left[ \begin{matrix} X_w \ Y_w \ Z_w \1 \end{matrix}\right] $$
其中,我们记 $ \bold{M}{3\times4} = \left[ \begin{matrix} \bold{K}{3\times3} & O \end{matrix}\right] \left[ \begin{matrix} R{3\times3} & T{3\times1} \ O & 1 \end{matrix}\right] $ 为相机的单应矩阵。
张氏标定法
保持摄像机位置不变,通过拍摄多张放置在不同位置的标定板的照片来估计相机的内参数与外参数。
标定板样例如下图所示:

每张图像中应至少包含5个角点,且至少拍摄3张不同位置的照片。
张氏标定法的主要流程如下图所示,详细流程可以参考张正友博士的论文$^{[5]}$或Encoder的知乎专栏$^{[6]}$。