DL01-常用的激活函数
神经网络的常用激活函数
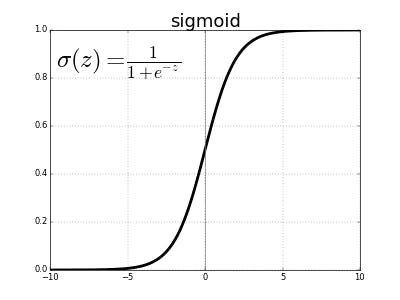
Sigmoid函数
解决二分类问题。 $$ f(z) = \frac{1}{1+\exp(-z)} $$ 其对应的导函数为 $$ f'(z) = f(z)(1-f(z)) $$
Tanh函数
$$ f(z) = tanh(z) = \frac{\exp(z)-\exp(-z)}{\exp(z)+\exp(-z)} $$ 其对应的导函数为 $$ f'(z) = 1-(f(z))^2 $$
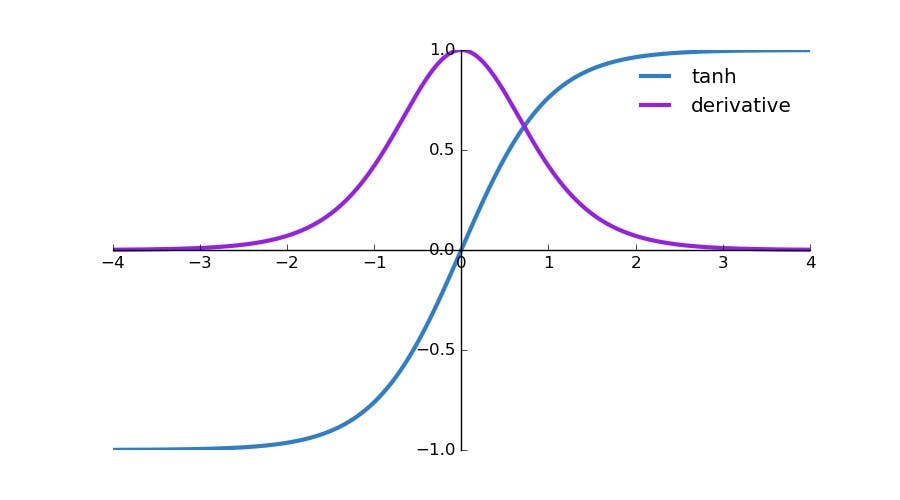
Tanh函数相当于Sigmoid函数的平移。
$\text{Tanh}(x) = 2 \text{Sigmoid}(2x)-1$
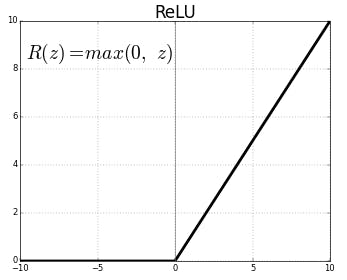
ReLU函数
$$ f(z) = max(0,z) $$ 其对应的导函数为
<img src="latex.codecogs.com/gif.latex?f'(z)=\left\{\begin{aligned}1,z>0\\0,z\leq&space;0\end{aligned}" title="f'(z)=\left\{\begin{aligned}1,z>0\\0,z\leq 0\end{aligned}" />
Leaky ReLu(LRelu)函数
<img src="latex.codecogs.com/gif.latex?f(z)=\left\{\begin{aligned}z,z>0\\az,z\leq&space;0\end{aligned}" title="f(z)=\left\{\begin{aligned}z,z>0\\az,z\leq 0\end{aligned}" />
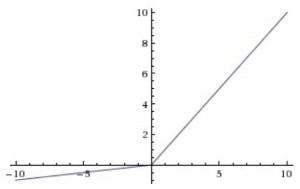
ReLU函数的变种,当$z\leq 0$时使用一个很小的正常数斜率$a$,即实现了单侧抑制,又保留了部分负梯度信息以致不完全丢失。
ReLu函数还有其他很多变种。
Softmax函数
将多分类任务的输出表示成概率。其输出值域为 $[0,1]$ 且结果之和必定为1。 $$ \sigma(\textbf{z})_j = \frac{ \exp(zj) }{ \sum{k=1}^{K}\exp(z_k) } $$
Sigmoid是针对二分类问题的极端情况下的Softmax。